[Algorithms] 비트 마스크 (Bitmask)

April 30, 2021 3 minute read

집합을 메모리&시간 효율적으로 다루는 방법.

정수의 이진수 표현을 자료구조로 사용한다.
집합 \(\{ A, B, C, D, E \}\) 의 부분집합 \(\{ C, E \}\)를 표현한다고 하면 \(10100_{(2)}\)가 된다.

1. 이점

빠른 연산속도

대부분의 연산이 O(1)의 시간복잡도를 갖는다.
ex) 특정 원소의 존재여부 판단시 선형탐색할 필요 없이 AND 연산 결과가 0보다 큰지 검사

메모리 효율적

vector<bool>의 bool 타입은 1바이트가 할당되지만, true 혹은 false를 저장하기 위해 1비트만 사용되므로 7비트는 낭비를 하고 있는 셈이다.

배열을 정수로 대체하므로 index로 활용 가능

엄밀히 말하면 C++ STL의 map<T,T> 컨테이너는 key값의 type으로 vector<T>도 허용하고 있기 때문에 기존의 배열 형태도 index로 쓰지 못하는 건 아니다.
그러나 bitmask로 배열을 표현해서 키값으로 사용했을 때 더 간결해지는 효과를 얻을 수 있다.

기존에 배열 형태의 key 값을 갖는 cache 변수가 있다고 하자.

map<vector<bool>,int> cache;

비트마스크를 이용하면 이렇게 간결해진다.

map<int,int> cache;

int cache[];

2. 비트 연산

기본

a & b    // AND    000101 & 000011 = 000001
a | b    // OR     000101 |  000011 = 000111
a ^ b    // XOR    000101 ^ 000011 = 000110
~a       // NOT   ~000101 = 111010
a << b   // SHIFT  000101 << 000011 = 101000
a >> b   // SHIFT  000101 >> 000011 = 000000

자주 하는 실수

연산자 우선순위 망각하기

bool a = (6 & 3 == 2);
// a = 0 (비교연산자 "==" 이 먼저 수행된다.)

정수 오버플로우 간과하기

bool isFlagUpBad(uint64_t a, int idx) {
  return (a & (1 << idx)) > 0;
} // 1은 int형. idx가 32보다 크면 오버플로우가 발생

bool isFlagUpGood(uint64_t a, int idx) {
  return (a & (1ull << idx)) > 0;
} // 여전한 제약조건: idx < 64

3. 집합의 표현

20 종류의 토핑이 있는 피자가 있다.

공집합과 꽉 찬 집합

uint32_t dough = 0;
// 0000 0000 0000 0000 0000 0000 0000 0000

uint32_t fullPizza = (1 << 20)-1;
// 0000 0000 0000 0000 0000 0000 0000 0001
// 0000 0000 0001 0000 0000 0000 0000 0000
// 0000 0000 0000 1111 1111 1111 1111 1111

원소 추가

pizza |= (1 << toppingIdx);

원소의 존재여부 확인

if (pizza & (1 << hamIdx)) {
  cout << "My pizza has ham on it !!\n"; // good
}

if ((pizza & (1 << hamIdx)) == 1) {
  cout << "naa..\n"; // bad. & 연산의 결과값은 1이 아니다.
}

원소 삭제

pizza &= ~(1 << toppingIdx);  // good
pizza -= (1 << toppingIdx);   // bad. 해당 bit가 원래 0이면 엄한 값이 된다.

원소 토글

pizza ^= (1 << toppingIdx);

집합 연산

uint32_t unionSet = a | b;      // 합집합
uint32_t intersection = a & b;  // 교집합
uint32_t removed = a & ~b;      // 차집합
uint32_t xor = a ^ b;           // 합집합에서 교집합을 제외한 집합

원소의 개수 계산

비트 하나씩 오른쪽으로 shift해주면서 1의 개수를 세어 준다.

int howManyToppings(uint32_t s) {
  int sz= 0;
  while (s) {
    sz += (s&1);
    s >>= 1;
  }
  return sz;
}

재귀로 해줘도 된다.

int howManyToppings2(uint32_t s) {
  if (s == 0) return 0;
  return (s & 1) + howManyToppings2(s >> 1);
}

최소 원소 찾기

uint32_t firstTopping= pizza & -pizza;
//          pizza = 01101100
//         -pizza = 10010100    two's complement
// pizza & -pizza = 00000100

최소 원소 지우기

uint32_t removed = pizza & (pizza-1);
//             pizza = 01101100
//           pizza-1 = 01101011
// pizza & (pizza-1) = 01101000

공집합을 제외한 부분집합 순회하기

uint32_t pizza;
for (int subset= pizza; subset; subset= (subset-1) & pizza) {
  // do something with subset
}
// subset = 01101100
// subset = 01101000
// subset = 01100100
// subset = 01100000
// subset = 01001100
// subset = 01001000
// subset = 01000100
// subset = 01000000
// subset = 00101100
// subset = 00101000
// subset = 00100100
// subset = 00100000
// subset = 00001100
// subset = 00001000
// subset = 00000100

4. 간단한 예제

15 퍼즐

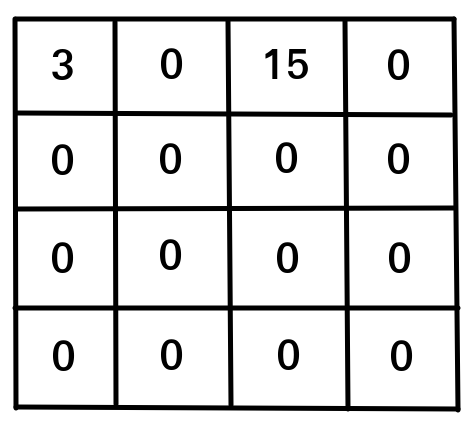
0 부터 15까지의 값을 갖는 4x4 크기의 퍼즐을 표현해보자.
가장 먼저 떠오르는 표현은 2D array이다.

int arr[4][4];

0 - 15 범위의 값만 가지므로 4비트씩이면 충분하다. 용량을 줄여보면,

char arr[4][4];

char 타입은 1바이트니까 여전히 4비트를 낭비하고 있고,
결정적으로 이렇게 해서는 이 상태를 인덱스로 쓰기가 번거롭다.

4비트 x 16개 = 64.
가장 깔끔한 방법은 uint64_t 타입의 bitmask다.

uint64_t bitmask;

\(arr[i][j]\)의 값을 가져오는 getter와 setter의 구현: bitmask
index를 표시해보면,

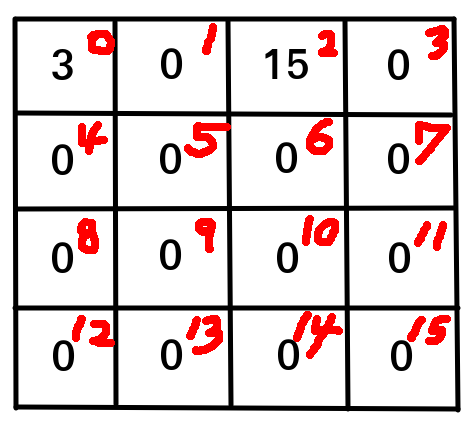
int getValue(uint64_t mask, int r, int c) {
  int idx= (r << 2) + c;
  return (mask >> (idx << 2)) & 15;
}

void setValue(uint64_t &mask, int r, int c, uint64_t value) {
  int idx= (r << 2) + c;
  mask= mask & ~(15ull << (idx << 2)) | (value << (idx << 2));
  //            ...111100001111...      ...0000{value}0000...
}

Junha Jeong