[LeetCode] 15. 3 Sum 풀이

Problem

15. 3 Sum

Approach

brute force 방식은 \(O(n^3)\)인데 \(0 \le nums.length \le 3000\).
계산이 \(9 \cdot 10^9\)번? (당연히) TLE가 난다.

첫 번째 인덱스 \(i\) 를 정하면 \(num[l] + num[r] = -num[i]\)인 \(l, r\) 값을 찾는 문제로 변한다.

배열을 정렬하고 각 \(i\)에 대해 two pointers를 아래처럼 수행한다.

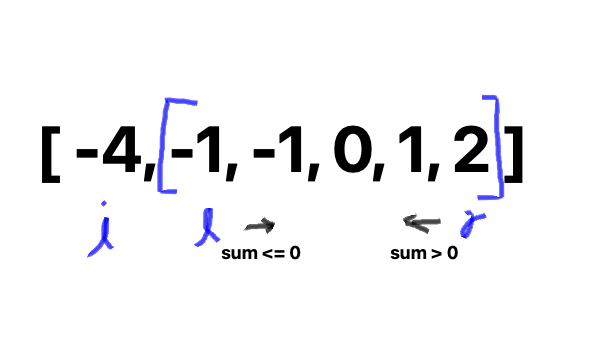
구현할때는 \(l, r\) 인덱스를 이동했는데 element 값이 그대로면 skip하도록 해서 불필요한 계산을 줄였다.

Code

/**
 * written: 2021. 12. 31. Fri. 16:46:01 [UTC+9]
 * jooncco의 mac에서.
 **/

typedef vector<int> vi;
typedef vector<vi> vvi;

class Solution {
public:
    vvi threeSum(vi &nums) {
        int n= nums.size();
        if (n < 3) return vvi();

        // 오름차순 정렬
        sort(nums.begin(), nums.end());

        // 순회하면서 two pointers를 수행
        set<vi> ans;
        for (int i=0; i < n-2; ++i) {
            int l= i+1, r= n-1;
            while (l < r) {
                if (nums[i] + nums[l] + nums[r] == 0) {
                    ans.insert({nums[i], nums[l], nums[r]});
                }

                if (nums[i] + nums[l] + nums[r] > 0) {
                    // 같은 값 skip
                    while (l < r-1 && nums[r-1] == nums[r]) --r;
                    // r을 왼쪽으로
                    --r;
                }
                else {
                    // 같은 값 skip
                    while (l+1 < r && nums[l] == nums[l+1]) ++l;
                    // l을 오른쪽으로
                    ++l;
                }

            }
        }
        return vvi(ans.begin(), ans.end());
    }
};

Complexity

• Time: \(O(n{\log}n + n^2)\)
• Space: \(O(n)\)