[LeetCode] 2203. Minimum Weighted Subgraph With the Required Paths explained

Problem

2203. Minimum Weighted Subgraph With the Required Paths

Approach

The shortest path of target subgraph falls into 3 forms:

1. src1 -> src2 -> dest
   

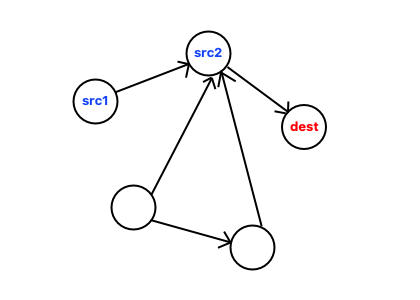
2. src2 -> src1 -> dest
   

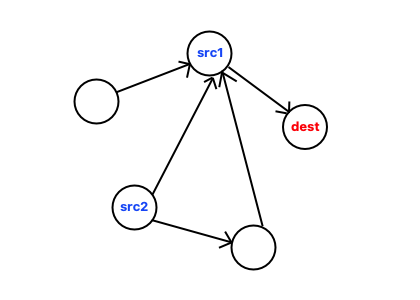
3. src1 -> dest, src2 -> dest (without sharing edges)
   

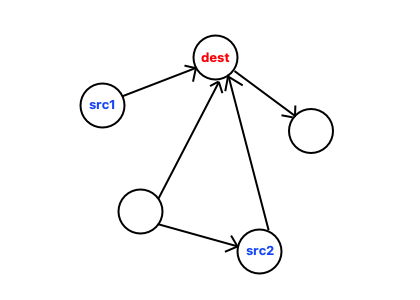
In every case, there always exists a vertex which two routes first join.
So we can generalize the process of finding shortest path as following:

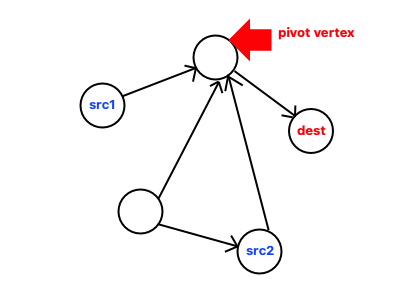
1. Find the shortest path from src1->pivot
2. Find the shortest path from src2->pivot
3. Find the shortest path from pivot->dest
4. Add 1, 2, and 3.

But how do we know which vertex is a pivot?

Run dijkstra 3 times with start node src1, src2, and dest(with inversed graph for this one). And then we simply linear search all the vertices, assuming current vertex is a pivot.

Each calculation takes \(O(1)\), thanks to precalculated shortest distances.

Note
use type long long to avoid integer overflow.

Code

#define f first
#define s second
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef deque<int> di;
typedef deque<ll> dl;
typedef priority_queue<int, vi, less<int> > maxHeap;
typedef priority_queue<int, vi, greater<int> > minHeap;

class Solution {
private:
    int N;
    ll INF= 1e12;
    vector<pii> adj[100010], adjInv[100010];

    vl dijkstra(int src, bool isInv) {
        vl dist(N,INF);
        dist[src]= 0;
        priority_queue<pll, vector<pll>, greater<pll>> pq;
        pq.push({ 0, src });
        while (!pq.empty()) {
            ll from= pq.top().s, curDist= pq.top().f;
            pq.pop();
            if (curDist > dist[from]) continue;

            for (pii &edge : (isInv ? adjInv[from] : adj[from])) {
                ll to= edge.f, cost= dist[from]+edge.s;
                if (cost < dist[to]) {
                    dist[to]= cost;
                    pq.push({ cost, to });
                }
            }
        }
        return dist;
    }

public:
    ll minimumWeight(int n, vector<vi> &edges, int src1, int src2, int dest) {
        N= n;
        for (int i=0; i < n; ++i) {
            adj[i].clear();
            adjInv[i].clear();
        }
        for (auto &edge : edges) {
            adj[edge[0]].push_back({ edge[1], edge[2] });
            adjInv[edge[1]].push_back({ edge[0], edge[2] });
        }

        vl d1= dijkstra(src1, false);
        vl d2= dijkstra(src2, false);
        vl d3= dijkstra(dest, true);
        ll ret= +INF;
        for (int i=0; i < n; ++i) {
            ret= min(ret, d1[i]+d2[i]+d3[i]);
        }
        return ret == INF ? -1 : ret;
    }
};

Complexity

• Time: \(O(n + \vert{E}\vert\log{n})\)
• Space: \(O(n)\)