[LeetCode] 309. Best Time to Buy and Sell Stock with Cooldown explained

Problem

309. Best Time to Buy and Sell Stock with Cooldown

Approach

There exists 3 states, and that can be expressed like this:

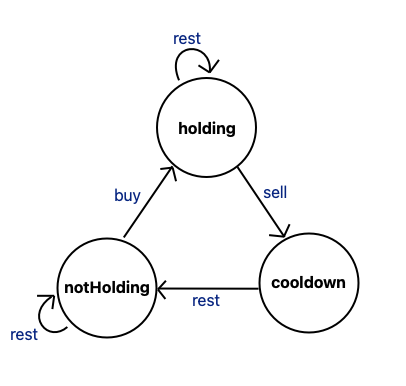
Hence, we can use dynamic programming approach to this problem, representing state transfers.

• holding[i] = max( holding[i-1] , notHolding[i-1] - prices[i])
• notHolding[i] = max( notHolding[i-1] , cooldown[i-1] )
• cooldown[i] = holding[i-1] + prices[i]

Initializing base case shouldn’t be difficult,

• holding[0] = -prices[0]
• notHolding[0] = 0
• cooldown[0] = \(-\infty\)

The ultimate answer is \(\max(cooldown[n-1], notHolding[n-1])\).

Note
We can optimize space complexity into \(O(1)\). Implementation below does that.

Code

typedef vector<int> vi;

class Solution {
private:
    const int NEG_INF= -1e7;
public:
    int maxProfit(vi &prices) {
        int n= prices.size(), holding= -prices[0], notHolding= 0, cooldown= NEG_INF;
        for (int i=1; i < n; ++i) {
            int prevHolding= holding;
            holding= max(holding, notHolding-prices[i]);
            notHolding= max(notHolding, cooldown);
            cooldown= prevHolding+prices[i];
        }
        return max(cooldown, notHolding);
    }
};

Complexity

• Time: \(O(n)\)
• Space: \(O(n)\)