[LeetCode] 53. Maximum Subarray explained

Problem

53. Maximum Subarray

Approach

Solution 1: DP

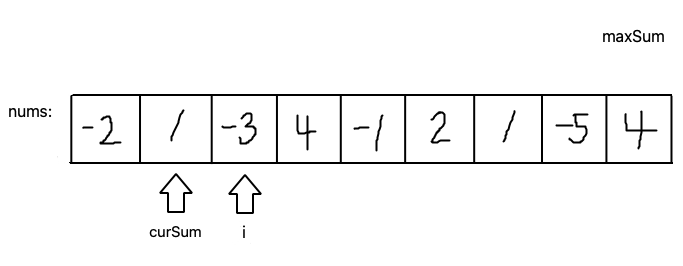
One pass from left to right.
While iterating the nums array, update curSum value with larger of those two.

• nums[i]
• curSum + nums[i]

The answer maxSum is the maximum value among all curSums.

Solution 2: Divide and conquer

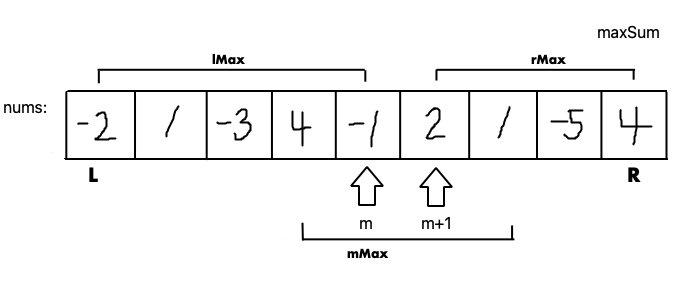
Think of the answer maxSum in a subarray nums[L:R]. It’s among those three.

• sum of subarray containing values nums[m] and nums[m+1] (mMax)
• maxSum in subarray nums[L:m] (lMax)
• maxSum in subarray nums[m+1:R] (rMax)

All we have to do is:

1. calculate the mMax
2. find maxSum in left and right subarrays (recursive call)
3. return max among those three

Code

Solution 1: DP

typedef vector<int> vi;

class Solution {
private:
    const int NEG_INF= -1e5;
public:
    int maxSubArray(vi &nums) {
        int n= nums.size(), ans= NEG_INF, curSum= NEG_INF;
        for (int i=0; i < n; ++i) {
            curSum= max(nums[i], curSum+nums[i]);
            ans= max(ans, curSum);
        }
        return ans;
    }
};

Solution 2: Divide and conquer

typedef vector<int> vi;

class Solution {
private:
    int maxSum(vi &nums, int L, int R) {
        if (L >= R) return nums[L];
        int m= L-(L-R)/2;
        // calculate maxSubarray containing nums[m] to the left
        int mMaxL= nums[m], lSum= nums[m];
        for (int i=m-1; i >= L; --i) {
            lSum += nums[i];
            mMaxL= max(mMaxL, lSum);
        }
        // calculate maxSubarray containing nums[m+1] to the right
        int mMaxR= nums[m+1], rSum= nums[m+1];
        for (int i=m+2; i <= R; ++i) {
            rSum += nums[i];
            mMaxR= max(mMaxR, rSum);
        }
        int mMax= mMaxL+mMaxR;
        return max( mMax, max( maxSum(nums, L, m), maxSum(nums, m+1, R) ) );
    }

public:
    int maxSubArray(vi &nums) {
        int n= nums.size();
        return maxSum(nums, 0, n-1);
    }
};

Complexity

Solution 1

• Time: \(O(n)\)
• Space: \(O(1)\)

Solution 2

• Time: \(O(N{\log}N)\)
• Space: \(O(1)\)