[LeetCode] 714. Best Time to Buy and Sell Stock with Transaction Fee explained

Problem

714. Best Time to Buy and Sell Stock with Transaction Fee

Approach

Solution 1: DP

There exists 2 states, and those can be expressed as:

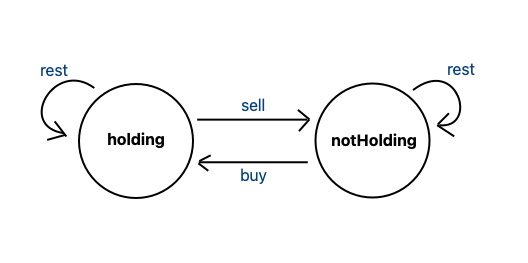
Hence, we can use dynamic programming approach to this problem, representing state transfers.

• holding[i] = max( holding[i-1] , notHolding[i-1] - prices[i])
• notHolding[i] = max( notHolding[i-1] , holding[i-1] + prices[i] - fee )

Initializing base case shouldn’t be difficult,

• holding[0] = -prices[0]
• notHolding[0] = 0

The ultimate answer is \(\max(holding[n-1], notHolding[n-1])\).

Note
We can optimize space complexity into \(O(1)\). Implementation below does that.

Solution 2: DP & Greedy

Example test cases tell us many things.

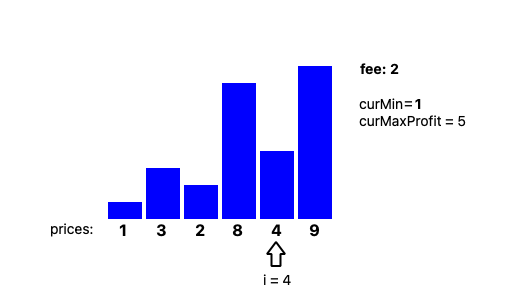
From left to right, update those values with following definitions.

• i: current index
• curMin: minimum price so far
• curMaxProfit: maximum profit so far

Say i=4, then curMin becomes 1 and curMaxProfit = 8 - 1 - 2(fee) = 5.
Here we need to decide wether to buy price[4] or not and it is always optimal to buy it when:
\(curMaxProfit + P - prices[i] - fee \gt P - curMin - fee\)
\(curMaxProfit + \bcancel{P} - prices[i] - \cancel{fee} \gt \bcancel{P} - curMin - \cancel{fee}\)
\(curMaxProfit \gt prices[i] - curMin\)
where P denotes some huge price in the future.

Thus, we can pick prices to buy in a greedy way, by checking the above condition.
From left to right,

• if \(curMaxProfit \gt prices[i] - curMin\), then ans += curMaxProfit. prices[i] is a new curMin now.
• else if prices[i] < curMin, update curMin value.
• else update curMaxProfit value

Code

Solution 1: DP

typedef vector<int> vi;

class Solution {
public:
    int maxProfit(vi &prices, int fee) {
        int n= prices.size(), holding= -prices[0], notHolding= 0;
        for (int i=1; i < n; ++i) {
            int prevHolding= holding;
            holding= max(prevHolding, notHolding-prices[i]);
            notHolding= max(notHolding, prevHolding+prices[i]-fee);
        }
        return max(holding, notHolding);
    }
};

Solution 2: DP & Greedy

typedef vector<int> vi;

class Solution {
public:
    int maxProfit(vi &prices, int fee) {
        int n= prices.size(), curMin= prices[0], curMaxProfit= 0, ans= 0;
        for (int i=1; i < n; ++i) {
            if (curMin + curMaxProfit > prices[i]) {
                ans += curMaxProfit;
                curMin= prices[i];
                curMaxProfit= 0;
            }
            else if (prices[i] < curMin) curMin= prices[i];
            else curMaxProfit= max(curMaxProfit, prices[i]-curMin-fee);
        }
        ans += curMaxProfit;
        return ans;
    }
};

Complexity

Solution 1

• Time: \(O(N)\)
• Space: \(O(N)\)

Solution 2

• Time: \(O(N)\)
• Space: \(O(1)\)