[Leetcode] 948. Bag of Tokens explained

Problem

948. Bag of Tokens

Approach

Sort the tokens array in ascending order.
Keep left and right indices, which denotes allowed tokens available with initialPower.

left \(\leftarrow\) 0
right \(\leftarrow\) n-1

While left <= right:

1. Find maximum score we can make with tokens in [left, right] and update maximumScore.
2. Subtract tokens[l] from initialPower and add tokens[r] to initialPower.
3. Increment left by 1, and decrement right by 1.

Return maxScore value in the end.

Sorting apparently takes \(O(n{\log}n)\).
The indices left and right covers all n tokens, and each time there is a computation with n-complexity.
Thie makes time complexity \(O(n^2)\).

Code

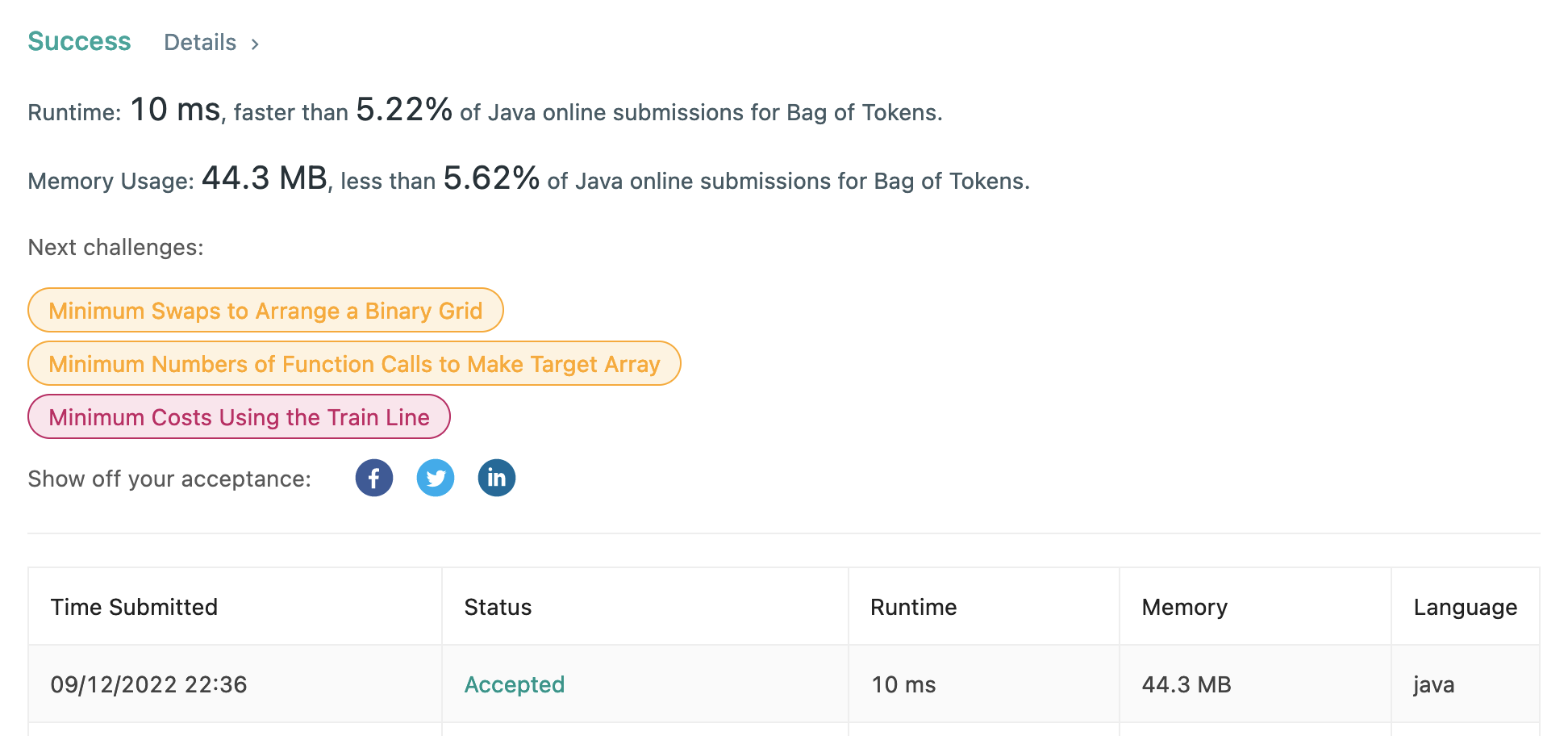
class Solution {
    public int bagOfTokensScore(int[] tokens, int initialPower) {
        Arrays.sort(tokens);
        int n= tokens.length, l= 0, r= n-1;
        int maxScore= 0;
        while (l <= r) {
            if (tokens[l] > initialPower) break;
            int idx= l, score= 0, power= initialPower;
            while (idx <= r && tokens[idx] <= power) {
                power -= tokens[idx++];
                ++score;
            }
            maxScore= Math.max(maxScore, score);

            initialPower += (tokens[r]-tokens[l]);
            ++l; --r;
        }
        return maxScore;
    }
}

Complexity

• Time: \(O(n{\log}n + n^2)\)
• Space: \(O(1)\)